ПОКАЗАТЕЛИ БЕЗОТКАЗНОСТИ ВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА

Время работы т элемента до отказа являет­ся случайной величиной, так как возникновение отказа — случайное событие. Пределы изменений внешних воздействий на элемент и ус­ловия его эксплуатации установлены документацией. Однако в этих допустимых пределах свойства самого элемента и режимы его работы изменяются случайно, что приводит к случайным моментам возник­новения отказов.

Последовательность событий, наступающих одно за другим в слу­чайные моменты времени, называют потоком событий. Если события заключаются в наступлении отказов или восстановлений, то имеет место соответственно поток отказов или поток восстановлений.

Поток событий называют ординарным, если вероятность попада­ния на произвольный интервал времени (t, I + At) двух (и более) со­бі, ітий пренебрежимо мала (равна нулю) по сравнению с вероятностью попадания одного события. Заметим, что величина At может быть значительной, притом тем больше, чем реже наступают события (чем нише безотказность элемента). Поток событий называют потоком без последействия, если вероятность попадания k событий на интервал (/, t + At) не зависит от числа и моментов появления событий на дру­гих, не пересекающихся с данным, участках.

Ординарный без последействия поток называют пуассоновским. Если события образуют пуассоновский поток, то число событий, по­падающих на любой участок (t, t — f — At), распределено по закону ред­ких событий или по закону Пуассона (см. табл. П.1). При этом веро­ятность того, что случайная величина X числа событий, попавших на интервал (t, t + At), принимающая значения 0, 1,2, …, т, равна т, выражается формулой

вер (X — т) = Рт = е~а, (2.1)

т!

где а — математическое ожидание числа событий, попадающих на а—09 33

интервал (t, t + At), которое называют параметром закона Пуассона. Параметр закона Пуассона может быть найден по формуле

(2.2)

где Ці) — интенсивность потока.

Если вероятность попадания k событий на интервал (t, t + At) зависит от числа k событий и длины интервала At, но не зависит от положения начала интервала t, то такой поток называют стационар­ным. Для стационарного потока интенсивность постоянна, т. е. по­стоянно математическое ожидание числа событий в единицу времени.

Пуассоновский стационарный поток называют простейшим, т. е. простейший поток обладает свойствами ординарности, стационарности и отсутствия последействия. Для простейшего потока число событий, попадающих на произвольный интервал длиной At, распределено по закону Пуассона с параметром

а = ХА t,

Время т между двумя соседними событиями в простейшем потоке — случайная величина, имеющая экспоненциальный закон распределения с плотностью

(2.4)

Строго говоря, для экспоненциальности распределения времени между двумя событиями требуются только стационарность и отсут­ствие последействия в потоке (см. [20J).

Перейдем к рассмотрению показателей безотказности невосста — навливаемого элемента, работоспособного в момент начала работы t == 0 и работающего до первого отказа, наступающего в случайный момент t = т. Такая модель работы элемента достаточно проста, и ее анализ позволяет легко установить ряд важных свойств.

Надежность введенного выше элемента полностью определяется его безотказностью, а показатели безотказности — характеристиками случайной. величины т, которую часто называют временем жизни эле­мента.

Как всякая случайная величина, время жизни элемента имеет закон распределения. Можно полагать, что величина т непрерывна, так как нельзя указать такие моменты времени, в которые отказ не был бы возможен. Обозначим функцию распределения величины т через

Q (t) = вер (т < t),

а плотность вероятности отказа — через

(2.6)

Кроме функции распределения (2.5) часто используют функцию надежности элемента

P(t) = 1 — Q(i) = вер(т> О,

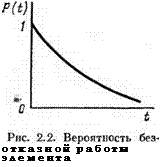которая представляет собой вероятность безотказной работы элемента за время t. Характерный вид функции показан на рис. 2.2. При t = О в соответствии с принятой моделью элемента (в момент включения ра­ботоспособен) имеем P{t = 0) — 1 и по логике при t—y — оо P(t}-> 0. Таким обра­зом, вероятность безотказной работы изме­няется в пределах от 0 до 1.

Для принятой модели элемента (работо­способный при включении, работающей непрерывно до первого отказа, происходя­щего в случайный момент времени) свой­ство надежности, как уже отмечалось, сво­дится только к безотказности, а безотказ­ность количественно характеризуется ве­роятностью безотказной работы за задан­ное время, принимающей значения от 0 до

I. В практике нередко говорят, что данный объект «имеет надежность 0,95». Это должно означать, что надежность объекта полностью сводится к безотказности и вероятность безотказной работы объекта за какое-то определенное время равна 0,95. Такое сокращение допустимо, если нет сомнений, что обменивающиеся ин­формацией хорошо понимают, о чем идет речь. Далее в книге также бу­дем использовать подобные упрощения, а строгие формулировки при­менять тогда, когда недостаточно очевидна решаемая задача.

Функции Q(t), q(t), P{t) являются исчерпывающими характеристи­ками случайной величины т, однако следует ввести и ряд других важ­ных параметров, определяющих безотказность элемента. Так, среднее время безотказной работы Т0, или средняя наработка до отказа (см. І24І), являющаяся математическим ожиданием случайной величины т, может быть найдена в виде

Д0 = Д4[т)== tq(t)dt. (2.8)

6

С учетом (2.6) и (2.7) имеем

оо оо оо

ть=*Ч(0dt = Iі —dГ dt = — JtdP(0- (2.9)

оо о

Интеграл (2.9) может быть взят по частям (t = и, dP(t) — dv). II предположении, что интегралы сходятся, получим

оо оо оо

— tdP(t) = —tP(t) I + P(t)dt. (2.10)

J об

Можно показать, что —tP(t) |"= 0, поэтому из (2.9) и (2.10) окон­чательно получим связь между средней наработкой до отказа и функ­цией надежности:

оо

T0-=P(t)dt. (2.11)

о

Таким образом, средняя наработка до отказа численно равна пло­щади под кривой P(t) на интервале (0, оо).

Следующим важным показателем безотказности невосстанавлива — емого элемента является условная, плотность вероятности возник­новения отказа, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не возник. Эту условную плотность вероятности возникновения отказа называют интенсив­ностью отказов, и по определению она связана с безусловной плот­ностью вероятности возникновения отказа q(t) следующим выраже­нием:

МО = q(0/P(0- (2.12)

Проделаем с последним выражением (2.12) некоторые очевидные преобразования, используя (2.7) и (2.6):

%(() = = —— ~~—> отсюда получим дифференциальное

уравнение

=^%(t)dt. (2.13)

Р (0

Проинтегрируем левую и правую часть от 0 до t:

ГТГ7= _ ІX(r)dr; 1пР(/) І* = — (М*)*.

6 о о о

так как P(t — 0) = 1 и 1пЯ (t — 0) = 0, то получим lnP(^) =

t

= — j Цт)с1(т) или

б

1

— | (г) dz

P(t) = e 0 . (2.14)

Для произвольного интервала (t±, 4) имеем

U

— j X (т) dz

P(tltt2) = e u. (2.15)

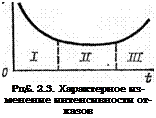
Функция МО для многих объектов имеет характерный вид (рис. 2.3) для разных периодов эксплуатации. Период / называют периодом приработки, в процессе которого устраняют систематические отказы элементов (конструкционные, производственные, эксплуатационные), заменяют элементы, имеющие дефекты. Все это приводит к повышению
вероятности безотказной работы и, следовательно, снижению интен­сивности отказов. В периоде //, часто называемом периодом нормальной работы, интенсивность отказов может оставаться постоянной, что приводит и к постоянной вероятности безотказной работы за заданное время. Наконец, в периоде III, называемом периодом старения и износа, интенсивность отказов увеличивается из-за необратимых физи­ко-химических процессов в элементе, связанных с его длительным использо­ванием.

Весьма важным для практики слу­чаем является работа элемента при по­стоянной интенсивности отказов. Это может быть обеспечено, если приработ­ка проведена до начала эксплуатации элемента, а срок службы исчерпывается до начала износовых отказов, опреде­ляющих повышение K(t). В случае, когда

X(t) = К = const, (2.16)

из (2.10) получим

P(t) = e-Kt.

Это выражение называют экспоненциальным законом времени жиз­ни элемента. Для него функция распределения в соответствии с (2.7) принимает вид

<3(0=1— ег-м, (2.18)

а плотность вероятности отказа при t> О

9(t)=^T = te*’ (2-19)

at

что совпадает с выражением (2.4).

С учетом (2.11) и (2.17) средняя наработка до отказа

оо

Т0= Je~^ # = -£-• (2.20)

о

Таким образом, математическое ожидание экспоненциального рас­пределения с плотностью вероятности 9(0 = ке~ХІ (О 0) равно 11%. Вычислим дисперсию этого распределения. По определению,

оо

Dlx] = M[т2] — (М[т])2 = j ПеГ"dt — (1 А)2- (2.21)

О

Интеграл в (2.21) является табличным (см. [26]):

ОО оо

о о

Нетрудно показать, что —/2е-х<|“ = 0. Тогда окончательно получим DM = 1/Х2 и а = / Шт] = 1/1. (2.22)

Таким образом, среднее квадратическое отклонение и математиче­ское ожидание экспоненциального распределения равны ПК.

Заметим, что интенсивность отказов обратна средней наработке до отказа только в том случае, когда — условие К — const выполняется на всем интервале (0, оо).

Для P(t) > 0,9 или Kt < 0,1 экспоненциальные зависимости (2.17),

(2.19) можно заменить приближенными формулами, основанными на разложении е~и в ряд до линейных членов:

P(f) » 1 — U Q(t) « П, q(t) « Я(1 — Kt). (2.23)

При такой замене наибольшая ошибка при Kt = 0,1 для P(t) не превышает 0,5%. Если такой точности недостаточно, то можно ввести в разложение нелинейный член:

P(t) « 1 — Kt + {Kt)V2; Q(f) » Kt — (Kf)*l2; q(t) » Ml — Kt + + (>./)2/2l. (2.24)

При использовании приближения (2.24) ошибка для P(t) при Kt — = 0,1 составит 0,01% , а при Kt = 0,2 составит 0,15%. В табл. 2.1 приведены точные и приближенные значения P(t), а также абсолютные ошибки для обоих приближений, рассчитанные соответственно по (2.17), (2.23) и (2.24).

Отсутствие последействия для отказов, подчиняющихся экспонен­циальному закону, приводит к тому, что вероятность безотказной ра­боты на данном интервале (t, t + Д7) не зависит от времени предшест-

Таблица 2.1 и р <0 Д ■ 10‘ и P(t) А • 10* 0,01 0,9000 0,15 0,8607 0,9000 0 0,8612 +5 0,9000 0 0,8500 — 107 0,05 0,9512 0 0,20 0,8187 0,9512 0,8200 +13 0,9500 — 12 0,8000 — 187 0,10 0,9048 0,9050 +2 0,9000 —48

вующей работы t, а зависит только от длины интервала т. Пусть эле­мент проработал безотказно на интервале (0, t). Тогда вероятность безотказной работы элемента на интервале (t, t + т) будет условной вероятностью того, что элемент проработал безотказно на интервалах (О, О и (/, t + т) при условии, что он был безотказен на интервале (О, t), т. е.

P(t, t+f) = P(t+ т )/Р (t) = е“х (/+х)/е_х* = е~Хх. (2.25)

Действительно, вероятность безотказной работы на интервале (t, t + т) зависит только от т.

Экспоненциальный закон широко используют в теории надежности, так как он достаточно прост и удобен, а также имеет определенную физическую основу. Однако его применение в каждом случае должно быть обосновано, потому что на практике часто имеют место более сложные законы возникновения отказов. К ним можно отнести законы Вейбулла, гамма-распределение, семейство нормальных законов и др., характеристики которых приведены в табл. П.1.